Power Law Exponent

The power law exponent (sometimes called the power law coefficient or simply 'alpha') is a number that characterizes the rate at which wind speed changes with height above ground. It is a parameter in the power law, which states that the wind speed varies with the height above ground according to the following equation:

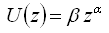
where:
	z	is the effective height above ground [m]
	U(z)	is the wind speed [m/s] at some effective height z
	b	is a constant
	a	is the power law exponent (alpha)

The graph below shows the effect of the power law exponent on the wind shear profile predicted by the power law. Each line on the graph corresponds to a different power law exponent, indicated in the graph with the symbol alpha, a. In all cases, the wind speed passes through 10 m/s at an effective height of 100m above ground.

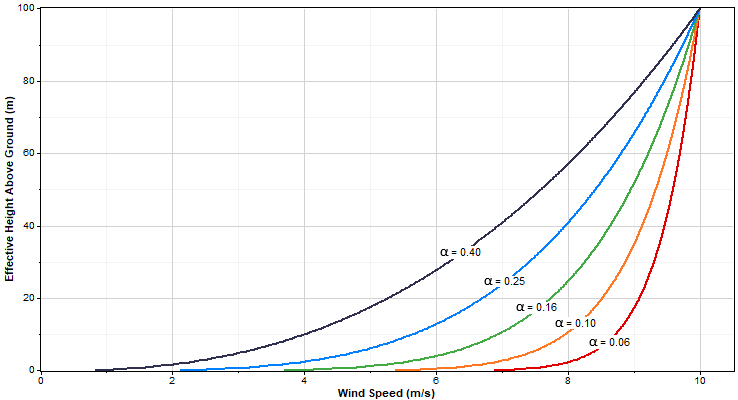
The power law exponent can be negative, indicating negative wind shear, meaning the wind speed decreases with height above the ground. In most places this is a rare atmospheric condition.

Calculating Power Law Exponent

For datasets containing wind speeds at two or more heights above ground, Windographer calculates the power law exponent that best fits the vertical wind speed profile. To see how, we need to do a little algebra. If we take the natural logarithm of both sides of the power law equation above, we get:

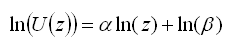
That equation is in the general slope-intercept form: y = mx + b, so if we were to plot ln(U(z)) versus ln(z), we would expect a straight line with slope equal to the power law exponent a, and the intercept equal to ln(b).

To demonstrate, let's begin by plotting wind speed versus measurement height from an uncommonly well-instrumented met tower with nine different measurement heights from 0.5m up to 80m:

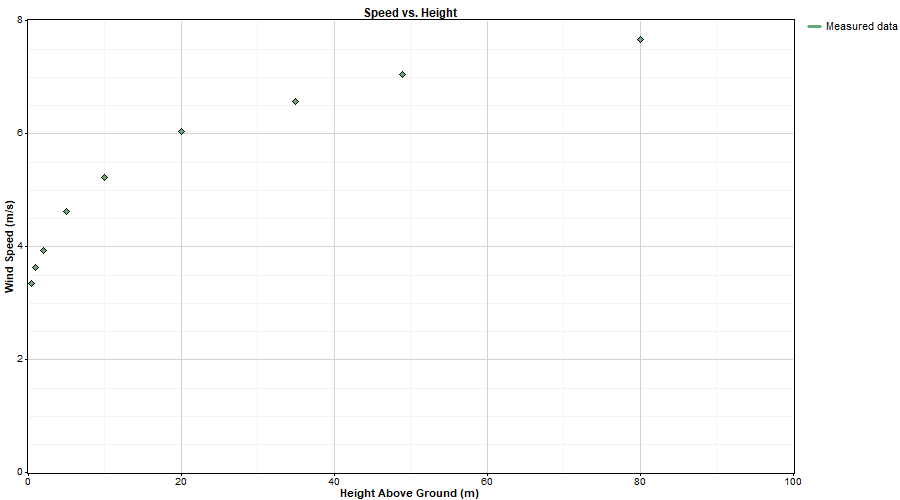
Now when we make both axes logarithmic we see a much more linear pattern:

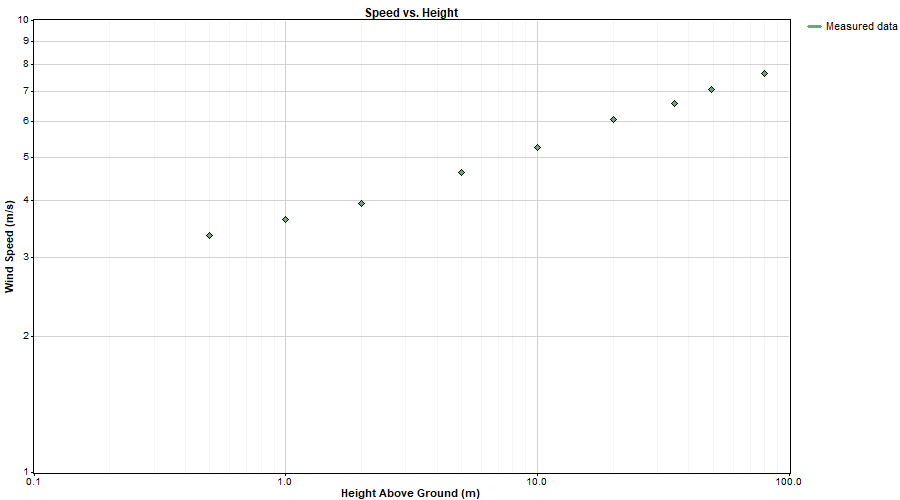
Using linear least squares we can fit a straight line whose slope is equal to the power law exponent:

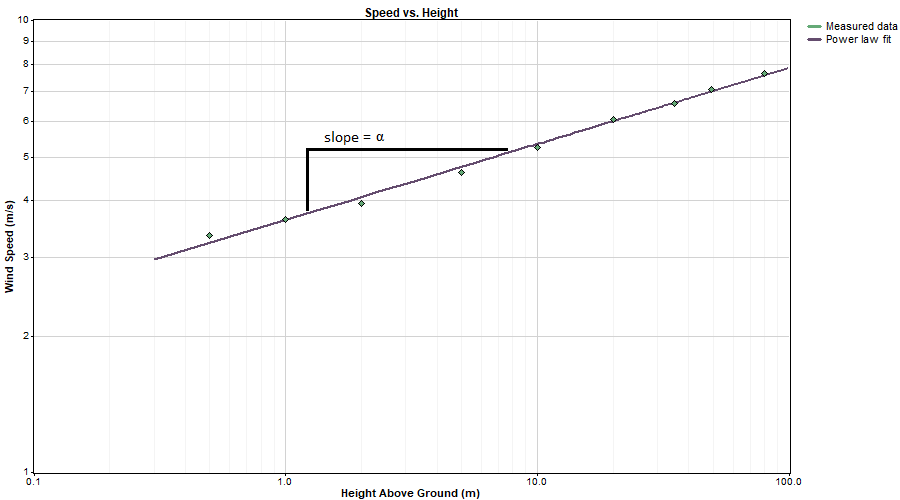
Windographer displays the overall best-fit power law exponent in the Dataset Summary table. In the Wind Shear window Windographer calculates the best-fit power law exponent versus month, time of day, direction, speed, and other factors, and reports the frequency histogram and extreme values as well.

Additional Considerations

If you have multiple wind speed sensors at exactly the same height, Windographer will fit the shear profile using a single average value at each available height.

Tip: In the Configure Dataset window you can create a calculated data column containing the power law exponent in every time step.