Linear Least Squares Algorithm

The 'Linear Least Squares' algorithm, also known as 'ordinary least squares' is a method of finding a linear relationship between the y and x variables in a set of (x,y) observations so as to minimize the sum of the squared errors measured vertically from the line of best fit, as illustrated below:

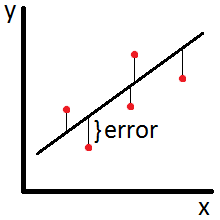
To implement the linear least squares algorithm on a set of N points of the form (x,y) Windographer first calculates the following intermediate variables:

Two-Parameter Fit

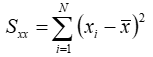
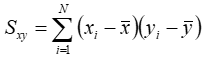
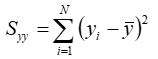
If we seek a linear fit of the form y = mx + b, where m is the slope and b is the intercept, then we can calculate the slope using the following equation:

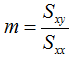
And the intercept using this equation:

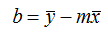
The following equation gives the uncertainty of the intercept:

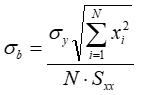
And the following equation gives the uncertainty of the slope:

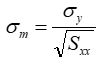
Where s_y, the uncertainty in the measurements, is given by the following equation:

One-Parameter Fit

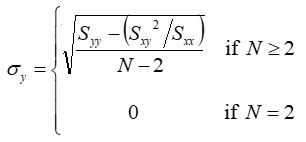
If you choose to force a zero intercept, the algorithm will solve for the best fit relationship in the form y = mx. In this case, Windographer calculates the slope using the following equation:

Consideration of Uncertainty

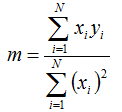
By focusing exclusively on the minimization of errors in the y dimension, the linear least squares algorithm effectively assumes that all uncertainty lies in the y-axis values. When this is an appropriate assumption, linear least squares is an appropriate algorithm. In contrast, when uncertainty can be equally attributed to both x-axis and y-axis values, the total least squares algorithm is usually more appropriate.