
| Linear Regression Trend Test |  |
The Linear Regression Trend Test is a test for the significance of a monotonic trend in a set of N values x1, x2, x3, …, xN, measured in chronological order at times 1, 2, 3, …, N.
This test fits a line to the mean values using the standard linear least squares procedure, where the x-values are the fractional year numbers corresponding to the middle of the annual, quarterly, or monthly periods, and the y-values are the means for each period.
To implement this test, we calculate the slope as usual with the two-parameter linear least squares algorithm:
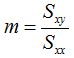
And we also calculate the uncertainty of the slope:
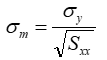
Where:
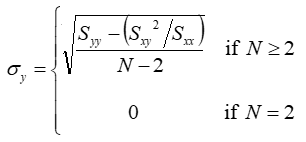
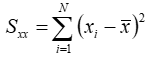
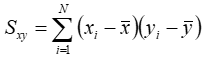
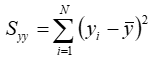
Then we calculate k, the multiplier that makes the confidence interval touch zero, by dividing the absolute value of the slope by the uncertainty in the slope:
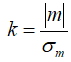
Then to determine the significance of the trend, we find P(<k), the percentile value of the standard normal distribution for the absolute value of that Z-statistic. P(<k) is the one-tailed significance, whereas the two-tailed significance is equal to 2 P(<k) – 1.
See also