
| Mann-Kendall Trend Test |  |
The Mann-Kendall test, described by Gilbert (1987) pp 209-213, is a test for the significance of a monotonic trend in a set of data.
We start with a set of N values x1, x2, x3, …, xN, measured in chronological order at times 1, 2, 3, …, N. Let j > i, and define sign(x) as a function that takes on the values 1, 0, or -1 as follows:
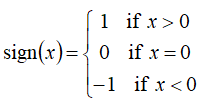
Now we calculate the sum of the sign of all changes S with the following equation:
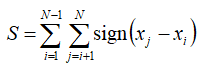
S is the total number of positive changes (from one measurement to a later measurement) minus the total number of negative changes. It will be positive if later observations tend to be larger than earlier observations, or negative if later observations tend to be smaller than earlier observations.
The following equations gives the standard deviation of this S statistic:
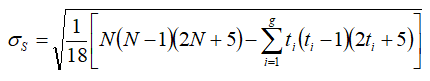
where: | ||
| g | is the number of groups of ties in the dataset | |
| ti | is the number of ties in the ith group of ties |
Now we define a Z-statistic using the following equation:
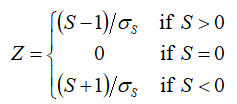
Then to determine the significance of the trend, we find P(<|Z|), the percentile value of the standard normal distribution for the absolute value of that Z-statistic. P(<|Z|) is the one-tailed significance, whereas the two-tailed significance is equal to 2 P(<|Z|) – 1.
See also