Standard Normal Distribution

The standard normal distribution is the normal (Gaussian) distribution with a mean of zero and a standard deviation of one. Windographer calculates the cumulative distribution function of the standard normal distribution using the following equation:

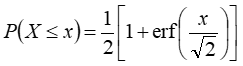
Where erf() is the error function.

Quantile Function

The equation below gives the quantile function of the standard normal distribution:

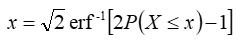
Windographer uses the quantile function to calculate the quantile corresponding to to a given probability. For example, to find the 99th percentile value, meaning the value that exceeds 99% of all values in the distribution, Windographer would use the quantile equation with a P(X ≤ x) value of 0.99, giving an x value of 2.326. That indicates that a value 2.326 standard deviations above the mean is greater than 99% of all the values in the distribution, assuming the distribution is normal.

The table below shows some other values of x produced by the quantile function.

P(X≥x)	x
0.500	0.000
0.841	1.000
0.900	1.281
0.990	2.326
0.995	2.576
0.999	3.090
0.9999	3.719
0.99999	4.265
0.999999	4.751