
| Total Least Squares Algorithm |  |
The 'Total Least Squares' algorithm, also known as 'orthogonal least squares', is a method of finding a linear relationship between the y and x variables in a set of (x,y) observations so as to minimize the sum of the squared errors measured orthogonally to the line of best fit, as illustrated below:
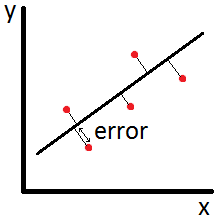
Tip: This method differs from linear least squares in its definition of the errors that it aims to minimize. Linear least squares defines errors as the vertical distance between each point and the line of best fit, whereas total least squares defines errors measured perpendicularly to the line of best fit.
To implement the total least squares algorithm on a set of N points of the form (x,y) Windographer first calculates the following intermediate variables:
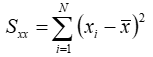
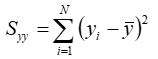
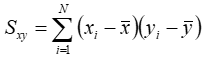
If we seek a linear fit of the form y = mx + b, where m is the slope and b is the intercept, then we can calculate the slope using the following equation:
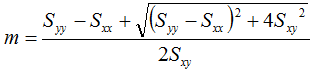
And the intercept with the following equation:
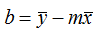
If you choose to force a zero intercept, the algorithm will solve for the best fit relationship in the form y = mx. In this case, Windographer calculates the slope using the following equation:
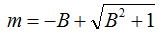
where:
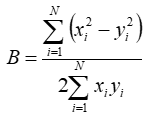
In its consideration of errors in both the x and y dimensions, the total least squares algorithm effectively assumes that x-axis and y-axis values are equally uncertain. When this is an appropriate assumption, total least squares is an appropriate algorithm. In contrast, when one can assume that only the y-axis values are uncertain, the linear least squares algorithm is usually more appropriate.
See also
Total Least Squares MCP algorithm