AWST Gust Factor Equation

AWS Truepower developed an equation, specific to 10-minute time steps, to approximate the gust factor for any gust averaging interval t:

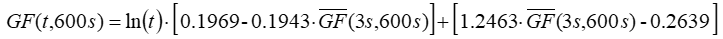
where:
	t	is the gust averaging time [s]
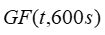		is the gust factor for 10-minute time steps for gust averaging time t [unitless]
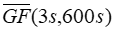		is the observed mean 3-second gust factor in the time series of 10-minute time steps [unitless]

To generalize this equation for use with any time step, we can divide GF(t,600s) by GF(T,600s), which is the output of the above equation setting t = T. The generalized form of the AWST gust factor equation is therefore:

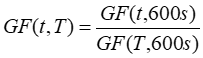
Note: the AWST gust factor equation produces a constant gust factor that does not change from one time step to the next. This contrasts with the other two gust factor equations Windographer implements, namely the extended Wieringa equation and the Gauss-Weibull equation, both of which produce a different gust factor in every time step because they depend on the turbulence intensity, which varies from one time step to the next.

Since the AWST gust factor equation uses the observed mean gust factor for three-second gusts and ten-minute time steps, we need to do some work before applying this equation to a time series in which the gust averaging interval is not three seconds, or the time step is not ten minutes. For this purpose, Windographer makes use of the Gauss-Weibull gust factor equation:

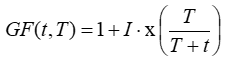
where:
	GF(t,T)	is the gust factor for any averaging time t and time step T [unitless]
	I	is the turbulence intensity [unitless]
	x()	is the quantile function of the standard normal distribution

For the specific case of t = 3s and T = 600s, the Gauss-Weibull equation gives:

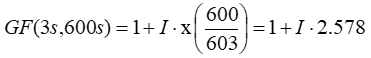
And if that is true, then we can use the following relation to estimate the average gust factor from the average turbulence intensity:

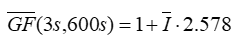
where:
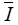		is the mean turbulence intensity, either calculated or assumed [unitless]

Windographer uses the above equation to calculate the mean 3-second, 10-minute gust factor for use in the AWST gust factor equation if the time series data lacks gust data or if the time step is not 10 minutes. The mean turbulence intensity value that Windographer uses in this equation depends on whether time series data includes turbulence intensity data. If so, then Windographer calculates the mean turbulence intensity value for speeds of 15 m/s and up. If not, it assumes a mean turbulence intensity of 0.10.

In the case of time series data that includes measured gust data at a time step other than ten minutes, Windograper scales the measured average gust factor by assuming that gust factors scale according to the Gauss-Weibull gust factor equation:

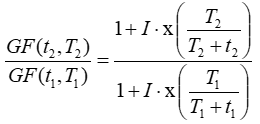
where:
	GF(t₁,T₁)	is the gust factor for averaging time t₁ and time step T₁ [unitless]
	GF(t₂,T₂)	is the gust factor for averaging time t₂ and time step T₂ [unitless]
	I	is the turbulence intensity [unitless]
	x()	is the quantile function of the standard normal distribution

Cross multiplying, setting t₂ = 3s and T₂ = 600s, and again assuming that the Gauss-Weibull equation can relate the mean gust factor to the mean turbulence intensity, we can write the following equation for the mean 3-second 10-minute gust factor as a function of the mean gust factor measured for any gust averaging period and any time step:

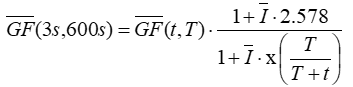
where:
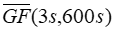		is the equivalent mean 3-second, 10-minute gust factor [unitless]
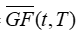		is the observed mean t-second gust factor in a time series with time step T [unitless]
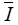		is the mean turbulence intensity [unitless]
	x()	is the quantile function of the standard normal distribution

Windographer uses the above relation when implementing the AWST gust factor equation in the case of time series data with measured gust factors at a time step other than ten minutes.

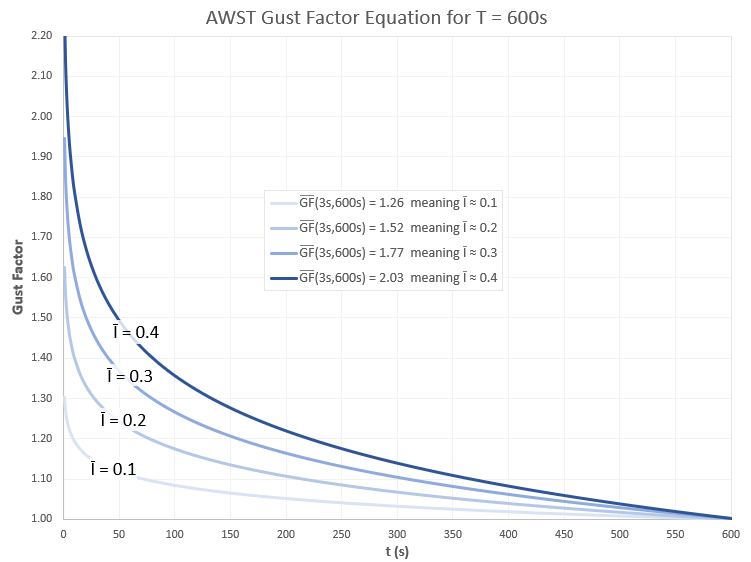
The graph below shows the output of the AWST gust factor equation for the case of ten-minute time steps, for a range of mean turbulence intensities, making use of the equation above that relates the mean 3-second 10-minute gust factor to the mean turbulence intensity:

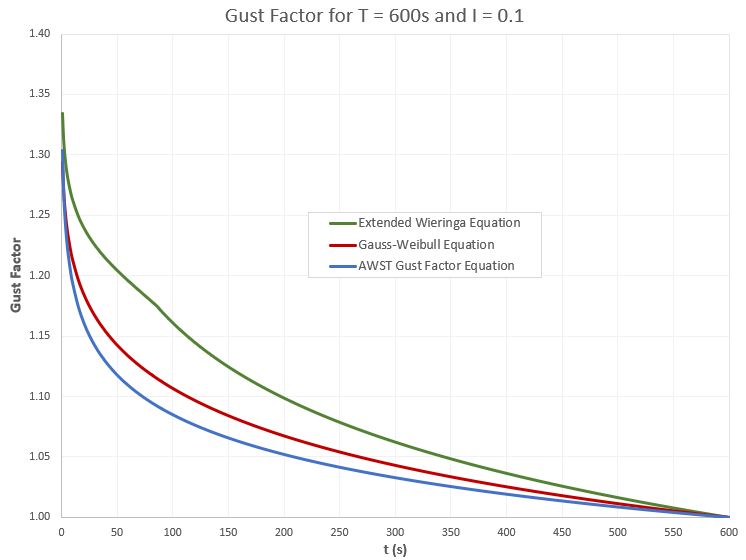
The graph below compares the AWST gust factor equation (again using the above equation relating the mean 3-second 10-minute gust factor to the mean turbulence intensity) to the other two gust factor equations Windographer implements, namely the extended Wieringa equation and the Gauss-Weibull equation, for the case of ten-minute time steps and 10% turbulence intensity: