
| Extended Wieringa Equation |  |
The Extended Wieringa equation gives the gust factor as a function of turbulence intensity, length of time step, and gust averaging time:
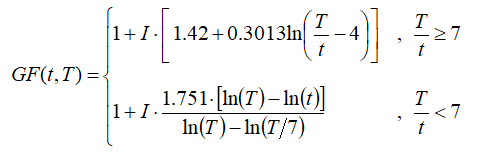
where: | ||
| T | is the length of time step [s] | |
| t | is the gust averaging time [s] | |
| I | is the turbulence intensity [unitless] | |
| GF | is the gust factor [unitless] |
Wieringa (1973) provides an equation to estimate the gust factor for any gust averaging time:
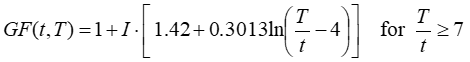
where: | ||
| GF(t, T) | is the gust factor for averaging time t and time step T [unitless] | |
| I | is the turbulence intensity [unitless] | |
| T | is the length of time step [s] | |
| t | is the gust averaging time [s] |
The above equation above does not appear explicitly in Wieringa's paper; it combines two equations that appear in the paper, specifically the one the paper refers to as equation 8:
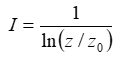
and the one the paper refers to as equation 10:
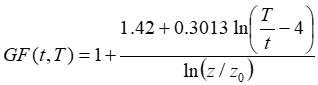
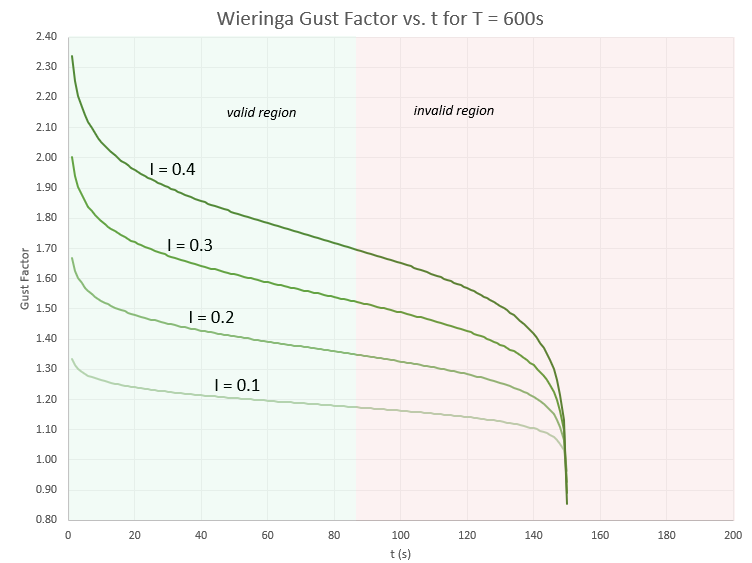
The Wieringa paper stipulates that the equation is valid only for gust averaging times less than one-seventh the time step. The graph below shows its behavior in the valid and invalid range of gust averaging times.
Windographer needs to be able to estimate gust factors for a wider range of gust averaging time, so we seek to extend this equation by switching to a logarithmic curve for gust averaging times greater than one-seventh the time step, meaning for (T / t) < 7. We therefore aim to develop a composite equation of the form:
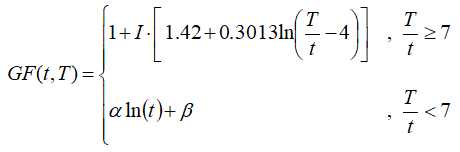
We will choose the two logarithmic curve fit parameters such that the two portions of the composite equation produce the same value at (T / t) = 7, and so that the gust factor drops to unity when t = T. We will therefore require the logarithmic curve to pass through two points, with the first at (T / t) = 7:
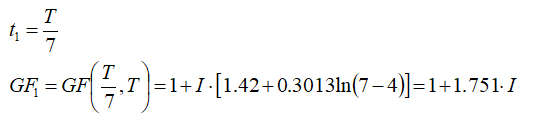
and the second point being at (T / t) = 1:

Now we can find our first curve fit parameter using:
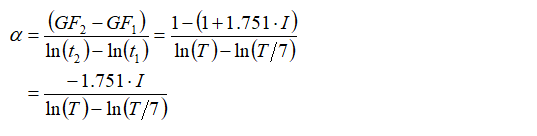
And using the second point on the logarithmic curve we can calculate the second curve fit parameter:

Now substituting these equations into our original proposed composite equation we can write:
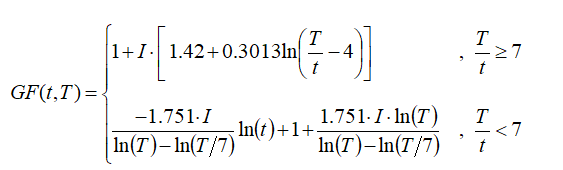
And we can simplify that to the following:
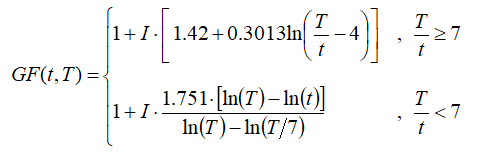
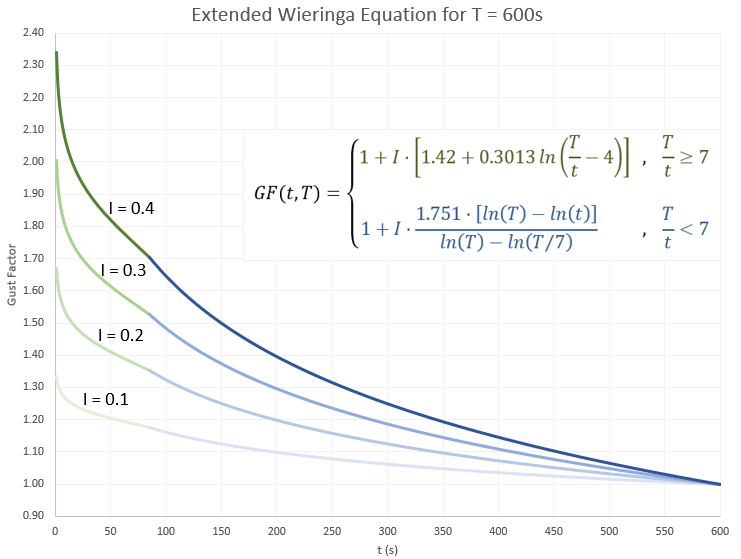
The graph below shows the results of the extended Wieringa equation for the case of ten-minute time steps (T = 600s) and four values of turbulence intensity. The green line segments come from the original Wieringa equation, whereas the blue line segments come from the logathmic extensions.
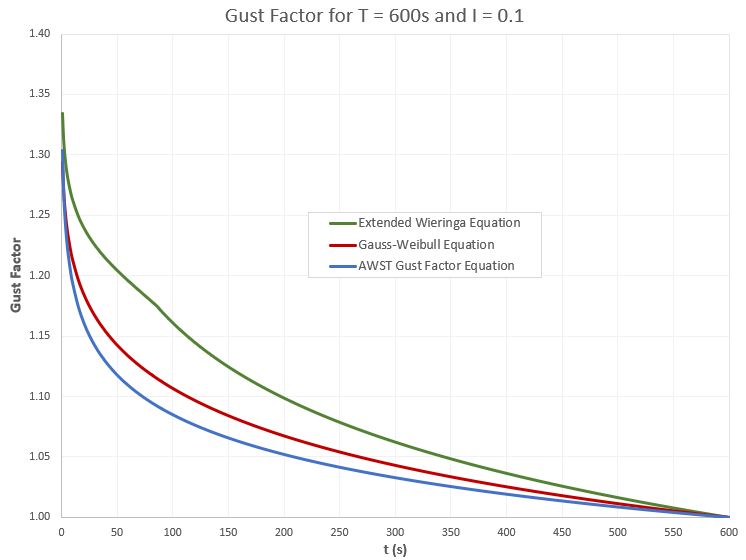
The graph below compares the extended Wieringa equation to the other two gust factor equations Windographer implements, namely the Gauss-Weibull equation and the AWST gust factor equation, for the case of ten-minute time steps and 10% turbulence intensity:
See also