Weibull Distribution

Wind analysts typically use the Weibull distribution to characterize the breadth of the distribution of wind speeds. The following equations give the probability density function and the cumulative distribution function of the two-parameter Weibull distribution:

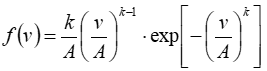
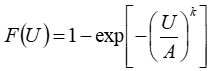
where:
	U	is the wind speed
	A	is the Weibull A factor (same units as U)
	k	is the Weibull k factor (unitless)

The following equation gives the relationship between the scale factor A and the long-term average wind speed:

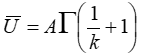
where:
	U	is the average wind speed
	G	is the gamma function
	k	is the Weibull k factor

The Weibull k value reflects the breadth of the distribution; the broader the distribution, the lower the value of the Weibull k. The graph below shows several Weibull distributions, all with an average wind speed of 7 m/s, but with the Weibull k value varying from 1.5 to 3.5.

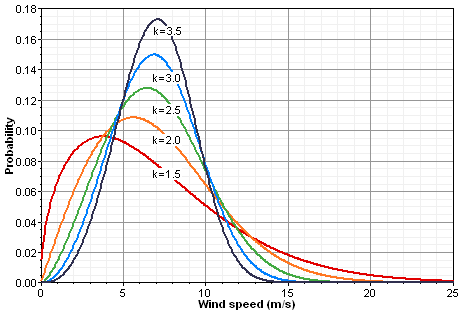
The Weibull distribution often fits measured wind speed distributions well. The graph below shows a measured wind speed distribution along with the best-fit Weibull distribution:

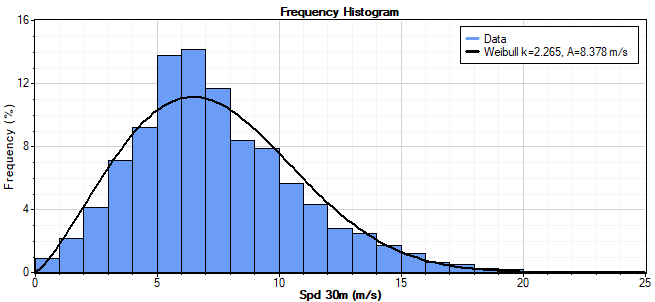
A Weibull fit algorithm is a method of finding the Weibull distribution parameters that best fit a set of observations. Windographer provides multiple Weibull fit algorithms, and in the Tools window you can choose your preferred Weibull fit algorithm.