Tower Distortion Factor

The tower distortion factor measures the degree to which the effects of tower distortion affect the relative output of two colocated wind speed sensors.

To calculate the tower distortion factor, Windographer calculates the ratio of the two wind speeds in each time step, bins those ratios by direction sector, finds their median value in each bin, and then calculates the weighted mean of the departure of those median values from unity. The following equation defines the tower distortion factor:

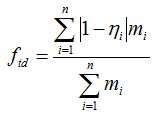
where:
	n	is the number of direction sectors
	h_i	is the median value of the ratios of wind speeds in direction sector i
	m_i	is the number of records in direction sector i

For the purposes of this calculation, Windographer divides the data into 72 direction sectors of 5° width each, so the value of n in the above equation is 72.

Since the tower distortion factor measures the departure from unity of the median ratio of two wind speed sensors, you can think of it as a measure of the 'area under the curve' of a plot of median ratio versus direction. This area under the curve appears highlighted in orange in the example graph below:

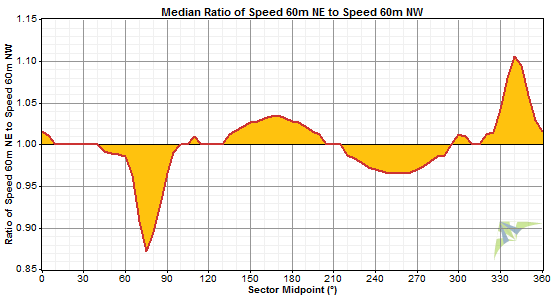
This analogy is not precise because the tower distortion factor is actually a weighted average of the departure from unity across all direction sectors, not the simple integral that this graphical analogy implies. But the graphical analogy helps illustrate the concept.

If the dataset exhibited no tower distortion, the median ratio versus direction graph would be a straight horizontal line along the y = 1 line, the area under the curve would be zero, and the tower distortion factor would also be zero. With greater and greater tower distortion, the median ratio line would deviate more and more from the y = 1 line, so the area under the curve would increase accordingly, as would the tower distortion factor.

We chose to base the tower distortion equation on median ratio values rather than mean ratio values because median values are less influenced by outliers. Wind speed datasets can include many erroneous wind speed values, including erroneously low wind speed values, which can lead to many spurious outlier values in the wind speed ratios. Basing this factor on median ratio values makes it less sensitive to such outliers.

Windographer displays this factor in the Tower Distortion window.

Tip: You can remove much of the effect of tower distortion by flagging tower shading events with the Flag Tower Shading window.