
| Scatter Factor |  |
The scatter factor measures the consistency over time of the output of two colocated wind speed sensors. To calculate the scatter factor, Windographer calculates the ratio of the two wind speeds in each time step, bins those ratios by direction sector, and measures their standard deviation in each bin. The following equation defines the scatter factor:
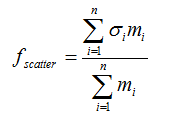
where: | ||
| n | is the number of direction sectors | |
| si | is the standard deviation of the ratios in direction sector i | |
| mi | is the number of records in direction sector i |
The scatter factor is therefore the weighted mean of the standard deviations measured in each direction sector. For the purposes of this calculation, Windographer divides the data into 72 direction sectors of 5° width each, so the value of n in the above equation is 72.
You may wonder why Windographer would consider wind direction at all in this calculation. The reason relates to tower distortion, which causes the mean ratio of the two wind speed sensors to vary by direction. We do not want that variation to affect the value of the scatter factor, because we want the scatter factor to reflect only the variation in time of the relative output of the two wind speed sensors.
By binning the wind speed ratios by direction sector, and then calculating the standard deviation within each bin, Windographer minimizes the effect of tower distortion on the scatter factor. If the scatter factor were instead based on the standard deviation of the entire set of wind speed ratios over all direction sectors, it would inappropriately conflate the effects of variation by direction and variation in time.
Since it reflects the variation in time of the relative performance of two wind speed sensors, a high value of scatter factor can indicate data quality problems caused by such issues as:
Windographer displays the scatter factor in the Tower Distortion window.
See also