Rule-of-Thumb MCP Uncertainty

Brower (2012) gives the following equation to estimate the uncertainty of the MCP process:

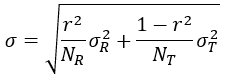
where:
	N_T	is the length of the period of record of the target (onsite) dataset [yr]
	N_R	is the length of the period of record of the reference dataset [yr]
	s_T	is the inter-annual variability of the target speed data [%]
	s_R	is the inter-annual variability of the reference speed data [%]
	r	is the Pearson correlation coefficient between target and reference data [unitless]

The target dataset typically only covers one or two years, which is insufficient to determine its inter-annual variability. Windographer therefore uses the assumption that the inter-annual variability of the target dataset is equal to that the reference dataset:

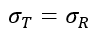
This equation is a 'rule of thumb' in the sense that it gives a reasonable prediction of the uncertainty of the MCP process based on some summary statistics. By contrast, the MCP algorithm performance test is a direct experimental measurement of the uncertainty of the process, based on the results of cross-validation rather than on an a priori prediction.