WAsP Algorithm for Weibull Fitting

The WAsP program has defined a requirement for fitting the Weibull distribution to measured wind speed data. The WAsP algorithm does not attempt directly to fit the measured frequency histogram, but rather requires that:

The mean power density of the fitted Weibull distribution is equal to that of the observed distribution.
The proportion of values above the mean observed wind speed is the same for the fitted Weibull distribution as for the observed distribution.

Let's take requirement number 1 first. The following equation gives the mean wind power density (WPD) of the Weibull distribution, assuming constant air density:

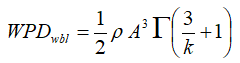
We can also write an equation for the mean power density of the observed wind speeds, again assuming constant air density:

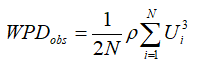
Requirement number 1 says that these must equate, so we can write:

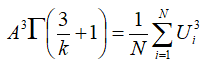
Solving this for A gives:

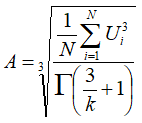(1)

Now for requirement number 2. We begin by defining a symbol X to represent the proportion of the observed wind speeds that exceed the mean observed wind speed. The cumulative distribution function F(U) gives the proportion of values that are less than U, so 1-F(U) is the proportion of values that exceed U. Requirement number 2 states that:

The following equation gives the cumulative distribution function of the Weibull distribution:

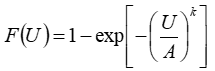
Since that equation holds for any wind speed U, it holds for the mean wind speed. So we can subsitute and rearrange to get:

So we can write:

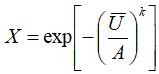
Taking the logarithm of both sides gives:

Now we can substitute equation (1) to get an equation whose only unknown is k:

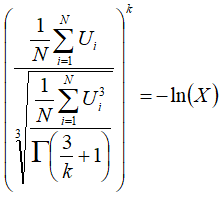(2)

When performing the WAsP algorithm to fit the Weibull distribution, Windographer first calculates X, then solves equation (2) iteratively, using the Brent method, to find the k parameter. Then it uses equation (1) to calculate the A parameter.