Openwind Algorithm for Weibull Fitting

The Openwind software uses a Weibull fit algorithm that finds the Weibull distribution meeting the following requirements:

The mean power density of the fitted Weibull distribution must match that of the observed wind speeds.
The mean wind speed of the fitted Weibull distribution must match that of the observed wind speeds.

Let's take requirement number 1 first. The following equation gives the mean wind power density (WPD) of the Weibull distribution, assuming constant air density:

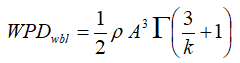
We can also write an equation for the mean power density of the observed wind speeds, again assuming constant air density:

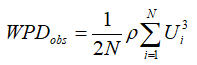
Requirement number 1 says that these must equate, so we can write:

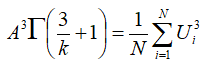
Solving this for A gives:

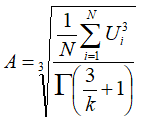(1)

Requirement number 2 says that the mean of the Weibull distribution:

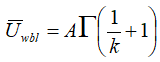
must equal the mean of the observed wind speeds:

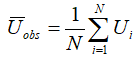
Therefore:

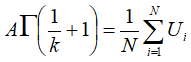
Solving that for A gives:

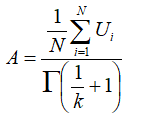
And equating that with equation (1) gives an equation whose only unknown is k:

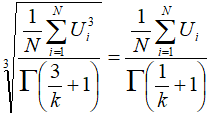(2)

When performing the Openwind Weibull fit algorithm, Windographer first solves equation (2) iteratively (using the Brent method) to find the k parameter. Then it uses equation (1) to calculate the A parameter.