Maximum Likelihood Algorithm for Weibull Fitting

The maximum likelihood method (Stevens and Smulders, 1979) fits a Weibull distribution to a set of measured wind speeds. This method employs the following equation to calculate, in an iterative fashion, the Weibull k parameter:

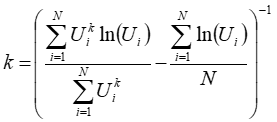
where:
	U_i	is the wind speed in time step i
	N	is the number of time steps

Once the shape parameter k has been found, the following equation gives the value of the scale parameter A:

Treatment of Low Wind Speeds

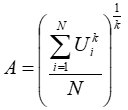
The above equation for k is undefined for zero wind speeds. To avoid zero and near-zero wind speeds, Windographer therefore implements the maximum likelihood method using the following steps:

Calculate the cutoff wind speed, which is the wind speed which the data exceeds all but 0.5% of the time.
Use the above equations to fit a Weibull distribution to the data that falls above the cutoff wind speed.
From the fitted Weibull distribution, draw random values between zero and the cutoff wind speed.
Use the above equations to fit a Weibull distribution to the combined data, meaning the original above-cutoff wind speeds plus the synthetically-generated low wind speeds.
Back to step 3 until the Weibull k value converges.