Least Squares Algorithm for Weibull Fitting

We can use a linear least squares algorithm to fit a Weibull distribution to measured wind speed data, but first we need to do some algebra. We start with the definition of the cumulative distribution function of the Weibull distribution:

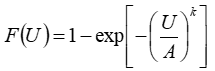
We can rearrange this to give:

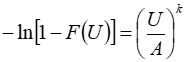
And using the rule ln(1/A) = - lnA, we can write:

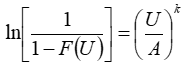
Taking the natural logarithm of both sides gives us:

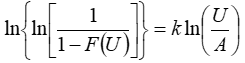
And using the rule ln(A/B) = lnA - lnB, we can write:

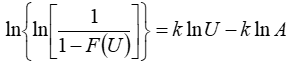
This equation is now in the general slope-intercept form: y=mx + b. Therefore, if we were to plot ln(U) on the x-axis and ln{ln[1/(1-F(U))]} on the y-axis, we would expect a straight line with slope equal to k and intercept equal to -k lnA.

Therefore, to find the best-fit Weibull distribution according to the least squares algorithm, Windographer calculates ln(U) and ln{ln[1/(1-F(U))]} for every data point, then puts those values into a linear least squares solver to calculate the slope and intercept of the line of best fit. It then sets k equal to the slope of that line, and A equal to exp(-intercept/slope).