
| Fix Quantization Window |  |
This feature is coming soon to Windographer 5.
The Fix Quantization window removes quantization from data by adding a random value to each data point in a way that respects the statistics of the original data.
The image below shows a histogram of heavily quantized data, whose values take only integer values. The histogram's bin width of 0.5 m/s results in every second bin containing zero data points. The fix quantization process in Windographer aims to add randomness to such a data sequence to produce a smooth frequency distribution that would not have empty bins even if the bin size were much smaller.
Quantization often results not from the fundamental properties of the data, but rather simply as a consequence of how the data are measured or stored. In the example above, the true wind speed certainly took on values between 4 m/s and 5 m/s, but at some point those true values were rounded to the nearest integer value, so that a value of 4.86 m/s changed to 5 m/s.
Obviously Windographer can't recover the 'true' original measurement values, as the quantization process discards that information. However it can still be advantageous in some situations to add randomness to recover the appearance of unquantized data. This tends to be true particularly when calculations depend strongly on the distribution of the data.
For example, when estimating extreme winds, Harris (1999) claims that the practice of rounding wind speed data to the nearest knot "... unnecessarily limits the accuracy of the data, and ... restricts the accuracy of the parameter estimates which can be made." He found that adding randomness to address the quantization improved the accuracy of his results. Likewise, King and Hurley (2004) recommended adding randomness to discretized data to improve the performance of MCP algorithms.
To address quantization in a data column, Windographer performs the following steps:
The goal of this step is to generate a histogram that contains no empty bins. Its bins can be of unequal size, but none can be empty. Therefore Windographer begins by generating a very fine histogram with small, equally-sized bins, then searches for empty bins that are adjacent to non-empty bins, and consolidates those empty bins with their neighboring bins. It continues to do this until no empty bins remain, meaning the non-empty bins have widened to the point that they touch each other, with no empty bins in between.
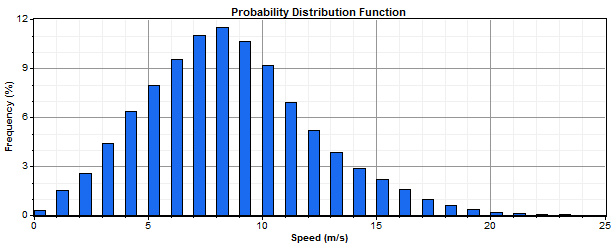
The resulting coarse histogram has bins that correspond closely with the quantization pattern of the original data. For example, if the original data contains only integer values, then the bins in the coarse histogram will center on or near the integers, with widths near one. Below appears an example coarse histogram for wind speed data that has been quantized to the nearest integer. Notice how each bin centers on an integer value, except for the first bin, which extends from 0 to 0.5 because wind speeds cannot be negative.

Windographer then calculates a target histogram by smoothing the coarse-grained histogram. This involves interpolating to bins where there originally was no data (due to the quantization of the original data) based on the overall shape of the coarse histogram. The resulting fine histogram is Windographer's best guess of the histogram of the 'true' data (prior to quantization) that you are trying to recover. This is the distribution that Windographer tries to attain when randomizing the data to remove quantization. The graph below shows an example of such a target histogram, generated from the coarse histogram above.
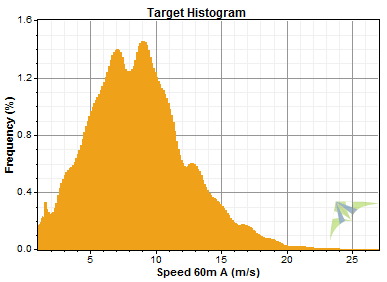
Finally, Windographer randomizes your original data such that the distribution of the final data fits the target histogram. In this step Windographer makes use of the coarse-grained histogram from step 1 to determine the spacing between quantized values, and therefore the range of random number values that it must add to the quantized values to eliminate the quantization. For example, if the original data is quantized to the integers then the spacing between each quantized value is 1.0, and the randomization process will add to each data point a random value in the range [-0.5, 0.5] (except for the first bin, as mentioned previously). Windographer uses the probability transformation technique to transform uniform random values into a set of random offsets that match the shape of the target histogram in this range. When these offsets are added to the data, the final distribution of the data will closely match the target histogram.
The image below shows an example of what the Fix Quantization window might look like. On the left appears the histogram of the original data, showing empty bins due to the high level of quantization. On the right appears the histogram of the randomized data after performing the above algorithm. The target histogram does not appear in this window, but generally the modified data fits the target histogram very closely.
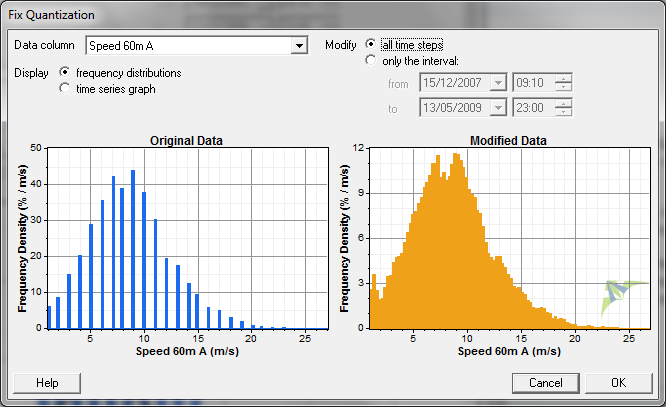
The before and after histograms may look quite different, but it is important to remember that Windographer achieves this effect by adding only very small offsets to your data. The graph below shows the same data used in the above image, only as a time series instead of a histogram. Note that the two data columns still look very similar, except that the orange line has been slightly offset at each point such that it is no longer restricted to take on only integer values.

See also