Probability Transformation

A probability transformation is a statistical procedure by which one modifies a set of numbers to conform to a desired probability density function.

To perform a probability transformation, Windographer first calculates the cumulative distribution function of the original set of data -- we will refer to this as the 'original CDF'. Then for each original data point, it performs the following steps:

It refers to the original CDF to calculate the percentile value corresponding to that original data point
It refers to the desired CDF to calculate the transformed value corresponding to that same percentile value

Example

Imagine that we have a set of data that conform to a normal distribution, and we want to transform it so that it conforms to a Weibull distribution. (Windographer does exactly this when synthesizing wind speed data.)

If our normally-distributed data had a mean of zero and a standard deviation of 1, its probability density function would look like this:

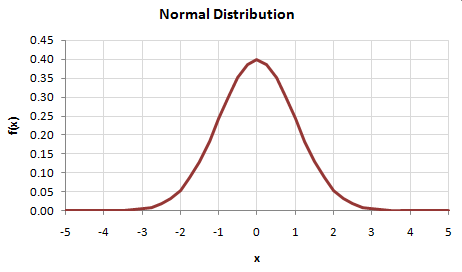
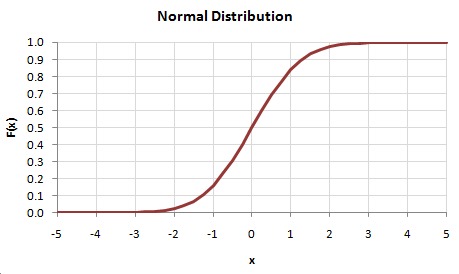
And its cumulative distribution function -- the original CDF -- would look like this:

Imagine that we wish to transform this data to fit a Weibull distribution with a mean value of 6 and a Weibull k value of 2. Our desired probability density function would therefore look like this:

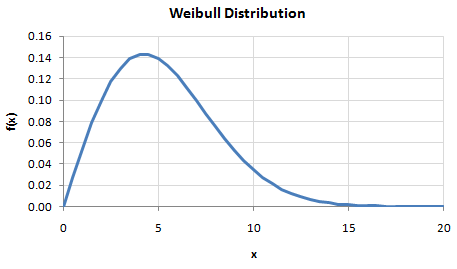
And our desired cumulative distribution function -- the desired CDF -- would look like this:

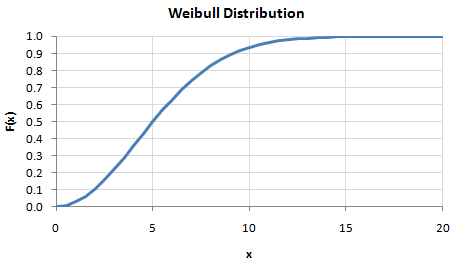
To transform each value in the original dataset, we would refer to the original CDF to find its corresponding y-value, then we would take that same y-value to the desired CDF and find its corresponding x-value.

An original value of zero, for example, corresponds to a CDF value of 0.5 on the original CDF. Looking at the desired CDF, we find that the value corresponding to a CDF value of 0.5 is approximately 5. That means that any zero value in the original dataset gets transformed into a value of 5 in the transformed dataset. Similarly, an original value of -1 would be transformed to a value of approximately 2.5, and an original value of 1.5 would be transformed to a value of approximately 10.

This example looks at transforming data from a normal distribution to a Weibull distribution, but with this same probability transformation approach, we could transform from any distribution to any other distribution.