
| International Standard Atmosphere |  |
The International Standard Atmosphere equations approximate the temperature, pressure, and air density in the atmosphere as a function of altitude. In the absence of measured temperature and pressure data, Windographer uses these equations to estimate temperature and pressure from the site altitude. Although the International Standard Atmosphere comprises layers that extend to the outer reaches of the atmosphere, Windographer only makes use of the lowest layer.
The following equation closely approximates the pressure of the International Standard Atmosphere up to an elevation of 5,000m:
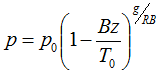
where: | ||
| p | is the air pressure [kPa] | |
| z | is the elevation [m] |
The following equation closely approximates the temperature of the International Standard Atmosphere up to an elevation of 11,000m:
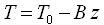
where: | ||
| T | is the air temperature [K] | |
| T0 | is the standard sea-level temperature [288.16 K] | |
| B | is the standard lapse rate [0.00650 K/m] | |
| z | is the elevation [m] |
Source for the above equations: Manwell et. al (2002).
Windographer uses the above equations to estimate air temperature and/or air pressure for any time step in which the dataset does not contain measured temperature or pressure data. (Temperature or pressure data may be missing either because the dataset does not include temperature or pressure data columns, or because these data columns contain gaps or have been flagged to exclude.) It does so in order to calculate the air density in each time step, which it then uses to calculate wind power density and wind turbine power output.
Explore the International Standard Atmosphere in the Standard Atmosphere tool window.
See also
Calculating the energy output of a wind turbine