Bootstrapping

Bootstrapping (Efron and Tibshirani, 1994) is a computational technique that measures the uncertainty of a process by performing that process repeatedly, with each iteration slightly different from the rest, and analyzing the distribution of results.

Bootstrap Datasets

Each iteration of the bootstrap involves generating a bootstrap dataset by randomly sampling the original dataset with replacement. Sampling with replacement is like pulling a name from a hat, putting it back in the hat, pulling another name, and so on. Because you keep putting the names back into the hat after pulling them, it's possible to pull the same name more than once. Each bootstrap dataset must contain the same number of samples as the original dataset.

For example, if this is our original dataset:

Then if we used sampling with replacement to generate five bootstrap datasets they might look like this:

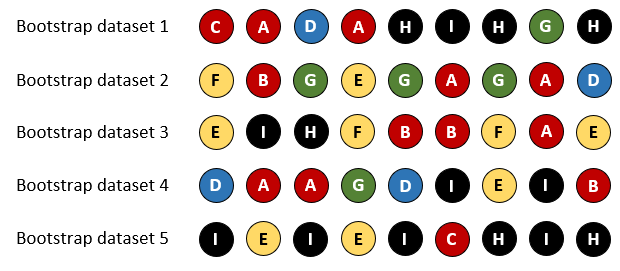
Each of the above bootstrap datasets contains the same number of values as the original dataset, and only contain values from the original dataset. If we generated many bootstrap datasets, we would expect the set of them to contain roughly the same number of red As, red Bs, blue Ds, and so on, but any particular bootstrap dataset may contain no blue Ds, or one blue D, or multiple blue Ds.

Using Bootstrapping to Estimate Uncertainty and Confidence Intervals

Simulating each of many bootstrap datasets produces many output values, the distribution of which tells us something about the uncertainty of the simulation process. If, for example, the original dataset is a set of (X,Y) points to which we intend to fit a regression line, then we could generate, say, 500 bootstrap datasets, fit a regression line to each, and then look at the 500 resulting slope and offset numbers. The standard deviation of those 500 slope numbers is a good estimate of the uncertainty in the slope, and the standard deviation of the 500 intercept numbers is a good estimate of the uncertainty in the intercept. The 2.5th and 97.5th percentile values of the slope numbers are a good estimate of the 95% confidence interval for the slope.

Windographer uses bootstrapping to estimate the uncertainty of the MCP process in the Test MCP Uncertainty window.