
| Markov Transition Matrix |  |
A Markov transition matrix is a square matrix specifying the frequency with which the values in a time series transition from one state to another when moving from one time step to the next.
To construct a Markov transition matrix, Windographer divides the range of values exhibited by a time series into N bins that serve as possible 'states' for that variable. Then it steps through the time series counting the number of times that the value transistions from state i in one time step to state j in the next time step.
Take for example the time series that appears below. It has a time step of 10 minutes, varies in value between zero and 100%, and covers an 18-month period, part of which appears in this graph:
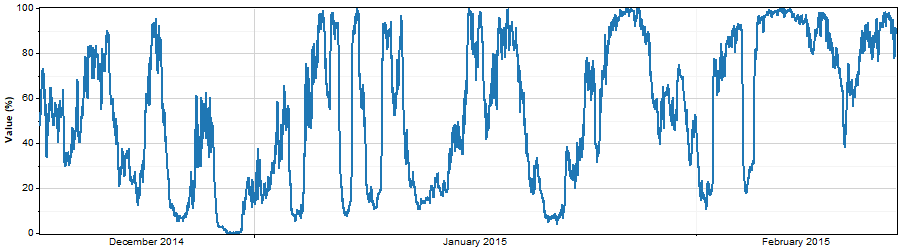
By dividing the range [0%, 100%] into 25 bins representing 25 states, Windographer calculated the following Markov transition matrix for this sample time series:
| Initial State | Final State | ||||||||||||||||||||||||
| 0%-4% | 4%-8% | 8%-12% | 12%-16% | 16%-20% | 20%-24% | 24%-28% | 28%-32% | 32%-36% | 36%-40% | 40%-44% | 44%-48% | 48%-52% | 52%-56% | 56%-60% | 60%-64% | 64%-68% | 68%-72% | 72%-76% | 76%-80% | 80%-84% | 84%-88% | 88%-92% | 92%-96% | 96%-100% | |
| 0%-4% | 0.861 | 0.125 | 0.010 | 0.002 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 4%-8% | 0.126 | 0.702 | 0.147 | 0.019 | 0.005 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 8%-12% | 0.005 | 0.130 | 0.694 | 0.146 | 0.017 | 0.004 | 0.002 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 12%-16% | 0.001 | 0.014 | 0.152 | 0.621 | 0.168 | 0.028 | 0.009 | 0.003 | 0.001 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 16%-20% | 0.001 | 0.005 | 0.021 | 0.134 | 0.607 | 0.180 | 0.034 | 0.012 | 0.003 | 0.002 | 0.001 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 20%-24% | 0.000 | 0.001 | 0.006 | 0.024 | 0.154 | 0.596 | 0.163 | 0.038 | 0.012 | 0.004 | 0.002 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 24%-28% | 0.000 | 0.001 | 0.002 | 0.010 | 0.031 | 0.153 | 0.581 | 0.168 | 0.035 | 0.010 | 0.005 | 0.002 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 28%-32% | 0.000 | 0.000 | 0.001 | 0.004 | 0.013 | 0.036 | 0.167 | 0.545 | 0.172 | 0.039 | 0.012 | 0.006 | 0.004 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 32%-36% | 0.000 | 0.000 | 0.000 | 0.003 | 0.007 | 0.017 | 0.046 | 0.166 | 0.519 | 0.171 | 0.037 | 0.018 | 0.006 | 0.005 | 0.002 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 36%-40% | 0.000 | 0.000 | 0.000 | 0.000 | 0.002 | 0.006 | 0.016 | 0.038 | 0.158 | 0.539 | 0.169 | 0.047 | 0.015 | 0.004 | 0.003 | 0.000 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 40%-44% | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.002 | 0.008 | 0.011 | 0.039 | 0.157 | 0.538 | 0.173 | 0.046 | 0.016 | 0.005 | 0.005 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 44%-48% | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.001 | 0.007 | 0.015 | 0.043 | 0.163 | 0.533 | 0.170 | 0.040 | 0.013 | 0.007 | 0.002 | 0.001 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 48%-52% | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.004 | 0.006 | 0.014 | 0.043 | 0.155 | 0.552 | 0.163 | 0.038 | 0.013 | 0.006 | 0.003 | 0.002 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 52%-56% | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.002 | 0.004 | 0.006 | 0.013 | 0.036 | 0.155 | 0.548 | 0.168 | 0.042 | 0.014 | 0.006 | 0.003 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 56%-60% | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.005 | 0.006 | 0.011 | 0.036 | 0.144 | 0.576 | 0.166 | 0.038 | 0.012 | 0.003 | 0.002 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 |
| 60%-64% | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.002 | 0.005 | 0.006 | 0.014 | 0.034 | 0.161 | 0.552 | 0.178 | 0.033 | 0.008 | 0.005 | 0.001 | 0.000 | 0.001 | 0.000 | 0.000 |
| 64%-68% | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.006 | 0.009 | 0.013 | 0.040 | 0.174 | 0.530 | 0.171 | 0.038 | 0.010 | 0.005 | 0.002 | 0.001 | 0.000 | 0.000 |
| 68%-72% | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.002 | 0.003 | 0.004 | 0.013 | 0.030 | 0.157 | 0.568 | 0.177 | 0.029 | 0.013 | 0.002 | 0.000 | 0.000 | 0.000 |
| 72%-76% | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.001 | 0.004 | 0.004 | 0.013 | 0.032 | 0.160 | 0.576 | 0.161 | 0.032 | 0.012 | 0.002 | 0.000 | 0.000 |
| 76%-80% | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.002 | 0.003 | 0.006 | 0.014 | 0.034 | 0.148 | 0.601 | 0.156 | 0.028 | 0.006 | 0.002 | 0.000 |
| 80%-84% | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.002 | 0.006 | 0.014 | 0.029 | 0.149 | 0.624 | 0.147 | 0.025 | 0.004 | 0.001 |
| 84%-88% | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.000 | 0.001 | 0.003 | 0.004 | 0.010 | 0.028 | 0.150 | 0.656 | 0.130 | 0.014 | 0.002 |
| 88%-92% | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.002 | 0.003 | 0.011 | 0.021 | 0.133 | 0.694 | 0.126 | 0.010 |
| 92%-96% | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.003 | 0.007 | 0.018 | 0.136 | 0.727 | 0.107 |
| 96%-100% | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.002 | 0.013 | 0.110 | 0.874 |
That transition matrix shows that if the value of the time series is in the 0-4% range in some time step, there is:
Similarly, it shows that if the value of the time series is in the 68-72% range in some time step, there is:
Windographer uses a Markov transition matrix as part of the Markov-based reconstruction mechanism.
See also
Markov-based reconstruction mechanism