
| EWTS II Algorithm |  |
The EWTS II algorithm is method for extreme wind speed estimation that appeared in the European Wind Turbine Standards II, (Dekker and Pierik, 1998). It takes a different approach than the other algorithms implemented in the Extreme Wind Analysis window. Like the others, this algorithm aims to estimate the 50-year extreme wind speed, but it is unique in that it does not consider any of the peak wind speeds recorded in the time series data. The only information it requires from the measured dataset is the mean wind speed and the Weibull k value.
The theoretical basis of the EWTS II algorithm is that if a set of wind speeds conforms to a Weibull distribution, then the Weibull k factor will determine the ratio of the extreme wind speed to the average wind speed. The algorithm comprises three variants, each of which uses a slightly different function relating that ratio to the Weibull k value. Windographer uses the names 'Exact', 'Gumbel', and 'Davenport' for these three variants of the EWTS II algorithm.
The Exact variation of the EWTS II algorithm uses the following equation for the ratio of the extreme wind speed to the average wind speed:
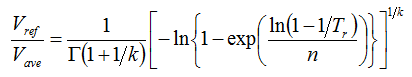
where: | ||
| Vref | is the extreme wind speed | |
| Vave | is the average wind speed | |
| G | is the gamma function | |
| k | is the Weibull k factor | |
| Tr | is the return period in years (50 if calculating 50-yr extreme values) | |
| n | is the number of independent events per year (23,037 for 10-min time steps and 1-yr extrema) |
The Gumbel variation of the EWTS II algorithm uses the following equation for the ratio of the extreme wind speed to the average wind speed:
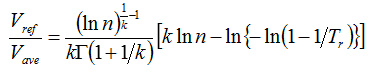
where: | ||
| Vref | is the extreme wind speed | |
| Vave | is the average wind speed | |
| G | is the gamma function | |
| k | is the Weibull k factor | |
| Tr | is the return period in years (50 if calculating 50-yr extreme values) | |
| n | is the number of independent events per year (23,037 for 10-min time steps and 1-yr extrema) |
The Davenport variation of the EWTS II algorithm uses the following equation for the ratio of the extreme wind speed to the average wind speed:
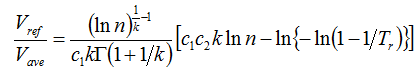
where: | ||
| Vref | is the extreme wind speed | |
| Vave | is the average wind speed | |
| G | is the gamma function | |
| k | is the Weibull k factor | |
| Tr | is the return period in years (50 if calculating 50-yr extreme values) | |
| n | is the number of independent events per year (23,037 for 10-min time steps and 1-yr extrema) |
And where the constants c1 and c2 are given by the following two equations:
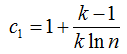
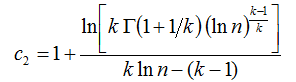
The following graph shows the results of each of the three variations, assuming 10-minute time steps and a return period of 50 years:
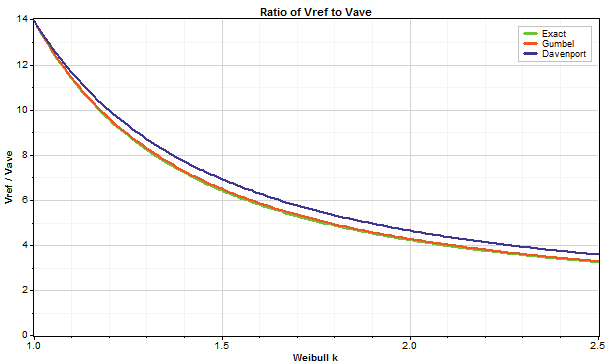
You can choose whether to use the overall average wind speed and the overall average Weibull k value, or the average and Weibull k value from just the windiest direction sector. Langreder et al. (2009) showed that using only the windiest sector can improve the accuracy of this algorithm.
The EWTS II tab of the Extreme Wind window implements the EWTS II algorithm.
See also