
| Variance Ratio Algorithm |  |
The 'Variance Ratio' algorithm is a simple and robust MCP algorithm proposed by Rogers et al. (2005). It uses a linear model of the form y = mx + b and it sets the two parameters of that linear model so that the variance of the predicted target wind speeds equals the variance of the observed target wind speeds.
This article uses x to denote observed reference wind speeds, y to denote observed target wind speeds. Using that notation, a linear model to predict target wind speeds from observed reference wind speeds appears as follows:
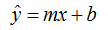
The Variance Ratio algorithm aims for the variance of the predicted target wind speeds to equal that of the observed target wind speeds, so:
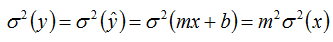
So the square of the slope is equal to the 'variance ratio', meaning the ratio of the variance of the observed target wind speeds to the variance of the observed reference wind speeds:
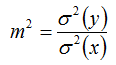
The slope itself is therefore equal to the ratio of the standard deviation of the observed target wind speeds to that of the observed reference wind speeds:
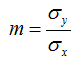
The Variance Ratio algorithm also aims for the mean of the predicted target wind speeds to equal the mean of the observed target wind speeds, so:
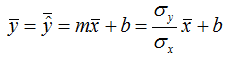
Solving that for the intercept yields:
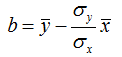
where x is the mean of the observed reference wind speeds and y is the mean of the observed target wind speeds.
If you choose multiple direction sectors, Windographer will subdivide the concurrent data by direction sector and calculate the slope and offset separately for each sector. It uses the reference direction sensor to determine the direction sector.
Similarly, if you choose multiple yearly divisions, Windographer will also subdivide the concurrent data according to month. If you choose 4 yearly divisions, for example, then January-March data will go in the first subdivision, April-June in the second, July-September in the third, and October-December in the fourth.
See also