
| Gumbel Distribution |  |
The Gumbel distribution is useful for modeling the probability of extreme wind speeds. The following equations give the probability density function and the cumulative probability distribution function of the Gumbel distribution:
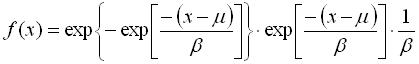
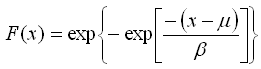
where x is the extreme value, b is a scale parameter, and m is a mode parameter. Both parameters have the same units as x.
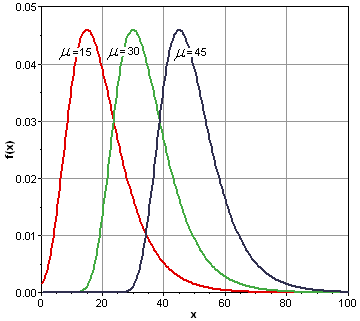
As its name implies, the mode parameter specifies the most probable value of x. The graph below shows the probability density function for three Gumbel distributions, all with a scale parameter of 8, but with the mode parameter varying from 15 to 45:
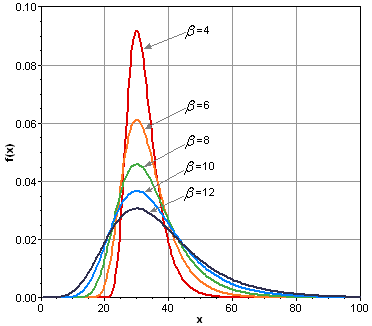
The scale parameter determines the breadth of the distribution. The graph below shows the probability distribution function for five Gumbel distributions, all with a mode parameter of 30 but with the scale parameter varying from 4 to 12:
The return period is a useful concept in the field of extreme value analysis. The return period is defined as the reciprocal of the probability of exceedence. For example, say that a given Gumbel distribution represents the distribution of annual extreme wind speeds, and that when x takes a value of 35 m/s, the cumulative distribution function F(x) gives a value of 0.9875. That means that there is a 98.75% probability that in any one year, the annual extreme wind speed x will be equal to or less than 35 m/s. The probability of exceedence of 35 m/s is therefore 100% - 98.75% = 1.25%. The resulting return period is 1 / 0.0125 = 80 years. That means that, on average, we would expect a wind speed of 35 m/s once in 80 years.
The following equation gives the annual extreme value for a specified Gumbel distribution and a return period of R years:
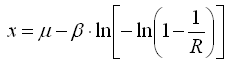
In the Extreme Wind window, Windographer fits a Gumbel distribution to the extreme wind speed data, and calculates the 50-year extreme wind speed using various algorithms.
See also