
Maximizing the revenue of a battery energy storage system is achieved through an optimal battery dispatch strategy. The optimal dispatch involves maximizing revenue by exporting energy from the battery or available renewable production and minimizing energy purchased to charge the battery, subject to physical constraints of the battery and any import or export limitations. The optimization problem of interest can be expressed as follows:
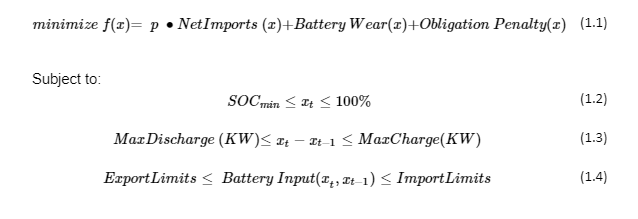
Term |
Description |
xt |
Battery state of charge (SOC) at timestep t |
P |
Energy market price |
Net imports |
The energy into or out of the system; net imports are negative when energy is exported, and positive when imported. This term reflects battery inputs, renewable production, converter and efficiency losses. |
Battery wear |
The wear cost depends on battery replacement cost and the battery charge or discharge at each timestep. |
Obligation Penalty |
Capacity market and time of delivery are treated as obligations that are penalized if not met. This term is 0 if capacity obligations are satisfied, positive otherwise. |
Import limits |
Available renewable production, interconnection limitations, as well as converter capacity limitations. |
Export limits |
Interconnection limitations and converter capacity limitations. |
|
|
Many theoretical algorithms are available for solving this class of inequality constrained optimization problems, where the proof of convergence requires meeting certain conditions at the solution. A nonlinear interior point method is used to solve this problem.
Dispatch Summary
Modeling battery dispatch involves the following steps:
i.Calculate the optimal dispatch over a 2-day horizon for a simplified battery model using the objective and constraints in Equation (1).
ii.Apply corrections to battery charge and discharge according to supplied battery model and apply degradation.
iii.Move optimization window forward 1 day using previous period to initialize the next window.
The dispatch is optimized over a two-day time horizon. The first 24 hours of the resulting dispatch are retained while the last 24 hours are used to initialize the next window. Using a time horizon that is longer than the optimization window ensures the battery has sufficient charge at the start of each period to take advantage of upcoming arbitrage opportunities and satisfy constraints.
The optimal dispatch incorporates several simplifications to the battery model to simplify the optimization problem. Then, a more exact model of the battery is applied to the optimized dispatch strategy to accurately model the system. For example, the charge and discharge constraints used in the optimization reflect the maximum possible charge and discharge the battery is capable of. Small adjustments are applied to the optimized dispatch to correct the charge and discharge according to the battery model parameters.
Additionally, battery degradation effects are not considered as dispatch decision variables. Degradation effects are applied to each time step of the supplied optimal dispatch instead. The 1-day optimization window is sufficiently small so that the applied degradation does not cause the modeled dispatch to significantly diverge from the optimized dispatch.
Multiple Energy Markets
Multiple energy market participation is not optimal because the market prices are not all known at the same time. Optimal modeling would produce an overly aggressive and unrealistic estimate. The goal, instead, is to produce a model that estimates the economic outcome of a skilled bidding strategy. More specifically, the goal is to produce estimates with reasonable relative accuracy so systems can be compared.
When there are multiple energy markets, an optimization is performed for each market. Each optimization involves one market and all of the other revenue streams and components, resulting in a desired storage dispatch. The two, or three, desired storage dispatches are then combined into a single dispatch.
Technically, later markets know about earlier markets, but bidding strategies often account for factors other than earlier market pricing, so it was found that modeling them without any knowledge of each other produced a more realistic result.
The dispatches are then combined according to a weighted decision scheme. For each time step, it is decided whether the BESS will charge or discharge. Markets that desired the decided dispatch direction are allowed to participate that time step and markets that desired the opposite are not. The amount of energy dispatched is calculated based on the desired dispatches of participating markets and their maximum storage commitments.
The BESS is then dispatched according to the Order of Commitment: Capacity Market first, then Time of Delivery, then Energy Markets. Energy is distributed only to Energy Markets participating this timestep, again weighted by desired dispatch and maximum storage commitment, and not to exceed maximum storage commitment.
PV and wind are also dispatched. All energy markets are included and distribution is made according to their allocations. The allocations are normalized if they add up to more than 100%.
For example, two markets could each have a maximum commitment of 100%. In time step 1, the first market could discharge 100% of the BESS and each market would sell 50% of PV and solar. In time step 5, the second market could now discharge 100% of the BESS and, again, each market would sell 50% of PV and solar. If both participate in a time step, the BESS distribution will be some combination based on desired dispatch and, again, each market would sell 50% of PV and solar.
Note that Energy Markets will not charge and discharge the battery in the same time step, sometimes referred to as virtual trading or buying out of a position. However, in certain circumstances, typically when a market has a negative price, one market could charge the battery while another market sells PV or wind.
See Also